El interés compuesto es uno de los conceptos más importantes, quizás sea el que más, del mundo de las finanzas. Ya lo dijo en su día Albert Einstein: El interés compuesto es la fuerza más poderosa de la galaxia. Esta frase nos da una idea del efecto que puede tener el interés compuesto sobre nuestro dinero.
Pero, ¿qué hay detrás de este concepto?
El concepto es muy sencillo: se trata de ir reinvirtiendo una determinada cantidad de dinero y la rentabilidad que nos va dando esta a lo largo del tiempo. Es decir, se necesita un doble esfuerzo de ahorro: por un lado la cantidad inicial con la que empezamos a ahorrar, y por otro evitar gastarse los intereses que esta inversión nos genera año a año.
¿Os hacéis una idea del dinero en el que se convierten 15.000 euros invertidos al 5% durante 25 años seguidos?
Estamos hablando de que esta cantidad de dinero se convierte en más de 50.000 euros. Estos serían los cálculos:

Probablemente pensareís que tal y como están las cosas es difícil ahorrar los 15.000 euros del ejemplo. O quizá sí tienes el dinero ahorrado, pero crees que vas a necesitarlo antes de 25 años. Por eso te animamos a que hagas tu propia simulación. Para ello, solamente teneís que aplicar la fórmula del interés compuesto:

Para realizar tu propia simulación necesitaréis desempoilvar vuestra calculadora financiera o abrir una hoja de Excel y calcularlo. No obstante, os vamos a poner algunos ejemplos de cuánto tiempo y cuánta rentabilidad anual necesitáis para duplicar vuestro dinero:
- 14 años y 2 meses invirtiendo a un 5%, o
- 7 años y 3 meses a una tasa anual del 10%, o
- 23 años y medio invirtiendo al 3%.
También podemos aplicar la regla matemática del 72, que aunque no es del todo exacta es muy sencilla y no tiene problemas para ser recordada. Si dividimos 72 entre una rentabilidad anual, obtendremos el tiempo necesario (en años) que tardarás en doblar tu capital.
Por ejemplo, para que 10.000 euros se conviertan en 20.000 se requiere invertir al 5% durante 14,4 años seguidos (72/5=14,4) y al 3%, 24 años (72/3=24). Como ves, el tiempo necesario es muy similar al de los ejemplos que indicamos más arriba.
¿Cuáles son las 3 claves para maximizar tus ahorros a largo plazo?
Como hemos dicho anteriormente, el poder del interés compuesto puede convertir una pequeña cantidad de dinero en una mucho mayor, siempre y cuando tengamos claras las 3 claves para maximizar nuestros ahorros a largo plazo:
Clave 1: Ahorro
¿De cuánto capital inicial dispongo? Y, ¿cuánto dinero puedo ir ahorrando poco a poco para añadir a mis inversiones? Y claro está que cuanto más dinero podamos invertir, mayor será la cantidad de la podremos disfrutar dentro de unos años, en términos absolutos. Para llegar a esta conclusión no hay que ser Einstein, que fue el que dijo que..
El interés compuesto es la fuerza más poderosa de la galaxia.
Pero si además de ir reinvirtiendo la rentabilidad obtenida por tus primeros ahorros, fuéramos añadiendo pequeñas cantidades cada X tiempo a esa hucha con la que queremos ahorrar para nuestra jubilación, para pagarle la universidad a nuestros hijos en el futuro o para comprarnos el Ferrari que siempre hemos querido.
En el ejemplo de abajo simulamos cuánto dinero podríamos obtener al cabo de 15 años si nuestro capital inicial es de solo 1.000 euros pero vamos ahorrando cada año otros 1.000 euros y añadiéndoselos a la hucha. Suponiendo una rentabilidad anual del 4%, el capital final sería de 20.825 euros:

Como cada año le vamos sumando 1.000 euros, es lógico que el capital final no sea el mismo que si hubiéramos tenido esos 15.000 euros de ahorro desde el principio. Es ese caso, el capital final hubiera alcanzado los 27.014 euros.

El ejemplo nos sirve para darnos cuenta de lo importante de ir ahorrando poco a poco.
Clave 2: Trata de maximizar la rentabilidad
¿En qué invierto mis ahorros?¿En depósitos?¿En la cuenta remunerada del mi banco?¿En bonos?¿En acciones…?
En esta segunda clave, lo más importante es tener en cuenta el RIESGO que implica estar invertido en acciones o estar invertido en depósitos, por ejemplo; y dentro de los depósitos, no es lo mismo tenerlo contratado con un banco que con otro, ya que no todas las entidades ofrecen lo mismo.
Cuando hablamos de riesgo entra en juego esa frase que hemos oído mil y una veces:
Nadie regala duros a cuatro pesetas.
Para comprenderlo de una manera amena, vamos a ver lo que dijo una vez el futbolista brasileño Elba de Pádua, que además de buen delantero dejó una frase digna de ser recordada:
El fútbol es una manta corta: si te tapas los pies te descubres la cabeza, y si te tapas la cabeza te descubres los pies.
En efecto, porque esa manta con la que comparó el fútbol también nos sirve para entender uno de los grandes condicionantes de las inversiones: la relación entre la rentabilidad y el riesgo. Si deseamos tener los pies bien calentitos (no asumir riesgos en tus inversiones), la cabeza va a quedar descubierta (menor rentabilidad). Sin embargo, si lo que queremos es tener la cabeza calentita (rentabilidades más atractivas), vas a tener que pasar frío en los pies asumiendo mayores riesgos. Algo muy importante de recordar es que en esto de las inversiones no existen mantas largas.
Una vez explicada la relación entre el riesgo que asumimos y la rentabilidad a la que aspiramos, veamos cuánto puede variar el capital final que logramos invirtiendo a largo plazo dependiendo de una mayor o menor rentabilidad anual.
Analicemos en primer lugar la diferencia que hay, por ejemplo, entre invertir 10.000 euros al 2,5% o hacerlo al 5%. El primer año es muy sencillo de calcular, la diferencia será tener 10.250 euros o tener 10.500. Pero, ¿y si durante 20 años invertimos a una u otra rentabilidad? Al 2,5%, a los 20 años tendríamos 16.385 euros, pero es que si hubiéramos obtenido durante ese tiempo una rentabilidad anual del 5%, el montante final ascendería a nada menos que 26.533 euros, es decir, más de 10.000 euros de diferencia:

Como vemos en el ejemplo, la rentabilidad es uno de los secretos para poder maximizar tus ahorros.
Clave 3: Invierte a largo plazo
¿Cuánto tiempo podré mantener mi inversión? Éste es quizá el concepto más sencillo de entender, ya que os obvio que cuanto más tiempo estemos invirtiendo, mayor rendimiento sacaremos a nuestros ahorros. Ahora bien, esto sucederá siempre y cuando la rentabilidad sea positiva; y decimos esto porque hay inversiones de las que no es que saquemos una rentabilidad muy baja, sino que directamente pueden hacer disminuir nuestro capital (por ejemplo si invertimos en acciones de una empresa que va mal y nos hace tener pérdidas).
¿Recordáis que en la primera parte del post sobre el interés compuesto vimos cómo 15.000 euros invertidos al 5% durante 25 años se multiplicaban por más de tres? Pues veamos, llegado ese punto, lo que supondría un año más invirtiéndolo:

¿Te das cuenta de la diferencia (en euros) que hay cuando empezamos a invertir con cantidades importantes? En el ejemplo comprobamos cómo los primeros 15.000 euros nos rentaban en un año 750 euros (considerando un 5% de rentabilidad). Pues bien, el premio a nuestra paciencia y esfuerzo de ahorro hace que pasados 25 años, esos 15.000 euros del principio pasen a rentarnos 2.540 euros cada año.
Al final va a ser verdad eso de que ”el dinero llama al dinero”…
Interés compuesto: Visión histórica
Tras ver qué es y para qué sirve el interés compuesto y el efecto exponencial que puede tener sobre nuestros ahorros, es hora de que veamos cómo funciona en la realidad.
¿Alguna vez os habéis preguntado cuánto se habría multiplicado nuestro dinero si hace 20 años hubiéramos invertido unos ahorros en bolsa? ¿Y si lo hubiéramos invertido en deuda pública? Y en ese periodo, ¿qué efecto habrá tenido la inflación en la rentabilidad real?
Rentabilidad de las diferentes clases de activo
Para realizar este análisis hemos estudiado cómo se han comportado varias clases de activo desde junio de 1995 hasta junio de 2015.
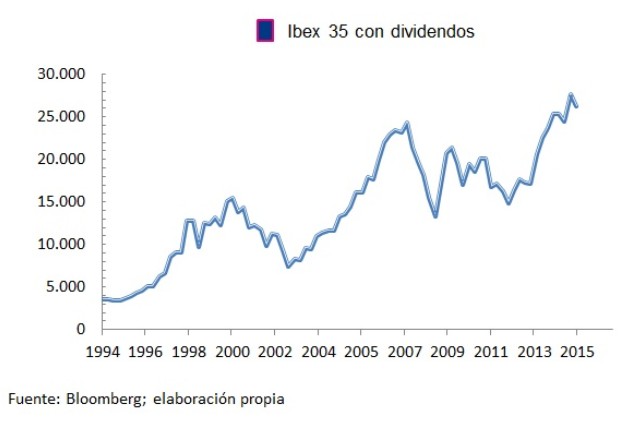
El índice Ibex-35 con dividendos se ha revalorizado una media de un 10,2% anual durante los últimos 20 años. Hemos escogido el índice Ibex-35 con dividendos y no el Ibex-35 porque el primero considera la reinversión en el Ibex de los dividendos que pagan sus empresas, por lo que representa mejor el comportamiento de la bolsa española.
Que el Ibex-35 se haya revalorizado de media un 10.2 % anual no significa que haya subido ese mismo porcentaje todos los años. Al ser un índice de bolsa ha sufrido muchas variaciones durante este tiempo, llegando a perder un -36% durante el año 2008 o a ganar un 47% en el año 1996. De ahí que a la bolsa, es decir, al mercado de acciones, se le denomine ‘renta variable’.
Si miramos a la bolsa americana, el índice S&P500 Total Return (que considera la reinversión de dividendos en el S&P500) se ha revalorizado una media del 9% en los últimos 20 años.
Si en vez de en bolsa hubiésemos invertido en deuda pública española, que a priori conlleva menos riesgo, la rentabilidad media anual desde 1995 baja hasta el 4,9%.
Según donde hubiese invertido alguien 10.000 euros (1.663.860 pesetas) hace 20 años, ahora tendría…

Rentabilidades pasadas no garantizan rentabilidades futuras
Las cifras de esta tabla son meramente orientativas, ya que nadie nos garantiza que la bolsa y la deuda pública se vayan a comportar de la misma manera en el futuro, cuando quizá estos mismos índices se comporten peor, mejor o igual. Lo que sí nos sirve es para ver cómo han evolucionado las diferentes clases de activo en las últimas dos décadas, lo que no deja de ser bastante representativo.
El efecto de la inflación y la importancia de la rentabilidad ‘real’
El dinero pierde valor con el paso del tiempo.
Lo que queremos hacerte ver es que lo verdaderamente importante es la rentabilidad real de una inversión, ya que no sirve de nada que un depósito me rente un 2% si la inflación es del 4%. En ese caso estaríamos perdiendo poder adquisitivo, es decir, con la misma cantidad de euros podré adquirir menos barras de pan, ya que la inflación provoca que el dinero vaya perdiendo valor con el paso del tiempo.
Según datos del INE (Instituto Nacional de Estadística), la inflación media de las dos últimas décadas ha sido del 2,4% anual. Esto quiere decir que si para pagar un número determinado de productos y servicios debíamos gastarnos 10.000 euros en 1995, en 2015 esta misma compra nos supone un desembolso de 16.070 euros.
Así pues, deberemos vigilar que la inflación no se coma la rentabilidad de nuestros ahorros. Lo más importante es que la rentabilidad media de nuestra inversión no sea inferior al dato de IPC vigente.
Estos datos tienen finalidad informativa y no deben interpretarse en ningún caso como una recomendación de compra o venta, o de realización o cancelación de inversiones, ni puede servir como base de ningún tipo de decisión sobre inversiones actuales o futuras. Self Bank no se hace responsable de los perjuicios que pueda sufrir el inversor como consecuencia del uso de dicha información. El Cliente es responsable de las decisiones de inversión que adopte y del uso que haga de la información proporcionada a tal efecto. Self Bank proporciona esta información a través de un proveedor y no asume compromiso alguno de la actualización en el contenido de la información presentada. La evolución o resultados pasados de las inversiones no garantizan la evolución o resultados futuros. Self Bank no acepta ningún tipo de responsabilidades por pérdidas, directas o indirectas, como consecuencia de este informe. Ninguna parte de este documento puede ser copiada o duplicada de cualquier forma o medio o redistribuida sin el previo consentimiento por escrito de Self Bank.


