¿Cuál es el rendimiento final que se obtendría de una inversión a dos años en la que se pierde un 50% el primer año y se gana 50% en el segundo? La respuesta que viene a la cabeza al 90% de la gente es 0.
En realidad, al final de dos años, se termina con una pérdida del 25%
Primer año: 100 * (1 – 50%) = 50
Segundo año: 50 * (1 + 50%) = 75
El efecto capitalización
Como se puede ver, la pérdida final es debido al hecho de que el retorno positivo del 50% del segundo año se calcula sobre una base más pequeña. Comenzando con un capital inferior, no se puede recuperar la pérdida del primer año que se calcula sobre el importe de la inversión inicial. A este hecho se le conoce como efecto capitalización.
Tratamos de representar este fenómeno utilizando una fórmula algebraica sencilla:
(1 – x) * (1 + x) = 1 – x2
Utilizando el ejemplo inicial, (1 – 0,5) * (1 + 0,5) = 1 – 0,52 = 0,75
Donde x representa el rendimiento obtenido en los dos años. Como puede verse, cuando una inversión tiene un resultado negativo y uno positivo iguales durante dos períodos, se obtiene un resultado final siempre menor a la inversión inicial (teniendo en cuenta que 1 se resta de la x2 número que es siempre positivo). Hubiera sido lo mismo si hubiéramos conseguido primero la ganancia y luego la pérdida.
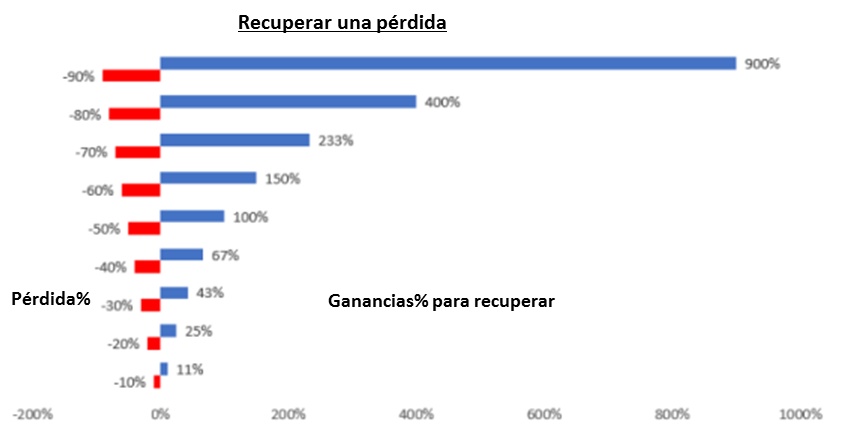
Este efecto crece al aumentar la amplitud del movimiento de los precios. Si x es igual a 10%, el efecto será igual a 1%, si x es el 50%, el 25% de la inversión se habrá erosionado en dos años por culpa de la volatilidad de los precios. De ello se desprende que, para volver en el equilibrio después de una pérdida, se requerirá una mayor proporción de beneficios respecto a la pérdida inicial. El mismo porcentaje no es suficiente para recuperar ya que partimos de una base menor.
Media aritmética vs media geométrica
¿Por qué la media aritmética no proporciona una representación verdadera sobre el resultado final de una inversión?
La media aritmética funciona bien cuando los eventos son independientes. Los rendimientos de una inversión no son independientes entre sí debido a que el rendimiento en un año determinado depende de la base del capital para el cálculo, y este viene de años anteriores.
La media aritmética, que es la que utilizamos en la vida cotidiana, se aplica cuando se suman n cantidades para producir un total. La media aritmética nos da el valor que las cantidades n tendrían que tener para que una vez sumadas diesen el mismo total en el caso que fueran todas iguales.
En cambio, la media geométrica se aplica cuando n cantidades se multiplican entre sí para dar un producto. La media geométrica es el valor que multiplicado por sí mismo n veces ofrece el mismo producto.
Debido a que el valor final de una inversión al final de n años es el resultado del producto (1+r1)*(1+r2)* …. *(1+rn), es la media geométrica de los rendimientos que se utiliza como un estándar para evaluar las inversiones. Esto tiene en cuenta el efecto de la capitalización, que se escapa de la media aritmética, y proporciona una representación exacta de la riqueza final del inversor.
La media geométrica de los rendimientos capitalizados se obtiene mediante la suma de 1 a los n rendimientos estimados, multiplicando entre ellos todos los (1 + r), mediante el cálculo de la raíz enésima del resultado y restando 1, el capital inicial.
r = ((1+r1)*(1+r2)* …. *(1+rn))1/n -1
En nuestro caso: (1.5*0.50)1/2 -1 = =-13.4%
La media aritmética de los rendimientos en nuestro ejemplo es igual a cero, pero en realidad al final de los dos años el inversor tiene en el bolsillo un 25% menos que la inversión inicial, que corresponde a un rendimiento geométrico anual del -13,4% y por lo tanto siempre hay que desconfiar de quien presenta una inversión con la media aritmética de los rendimientos anuales.
La volatility drag
La media aritmética es siempre mayor que la media geométrica excepto en el caso en el que los rendimientos anuales son constantes. Tomemos un ejemplo en el que los rendimientos durante dos años consecutivos han sido del 5%:
La media aritmética es (5%+5%)/2 = 5%.
La geométrica es (1.05*1.05)1/2-1 =5%
En este caso, es decir cuando la volatilidad de los rendimientos es cero, las dos medias son iguales. En cualquier otro caso, la volatilidad tiende a reducir el retorno geométrico, aquel que realmente recibe el inversor.
La diferencia entre la media aritmética y la media geométrica de los rendimientos se llama volatility drag.
Volatility drag = Rendimiento aritmético – Rendimiento geométrico
En el caso de rendimientos distribuidos de una manera normal, el efecto de la volatility drag se aproxima a:
Volatility drag= 0.50 * Volatilidad2
Donde la volatilidad viene dada por la desviación estándar de los rendimientos. La prueba matemática de este resultado está fuera del alcance de este post.
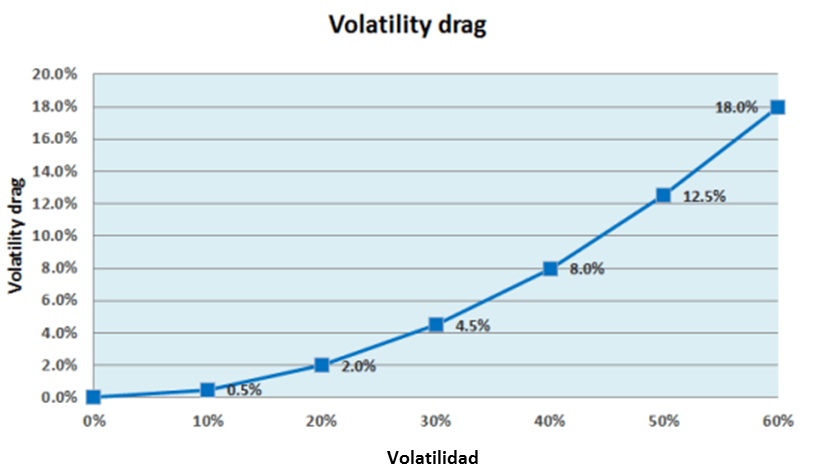
Por la misma media aritmética de la rentabilidad, el rendimiento geométrico disminuye al aumentar la volatilidad.
Desde 1926 hasta hoy la rentabilidad media del S & P 500 fue del 12% mientras que el rendimiento geométrico fue del 10%. Con una volatilidad del orden del 20%, el peso de la volatility drag en la media geométrica está en línea con la prevista por la fórmula (0.2 ^ 2/2 = 2%).
El uso de órdenes de stop loss
A estas alturas debería ser evidente porque se aconseja siempre evitar grandes pérdidas a través del uso de órdenes de stop-loss. Cortando las pérdidas antes de que estas se acumulen evitamos grandes reducciones del capital que, a través de la capitalización de los rendimientos, pesaría sobre el rendimiento final.
La anomalia de las acciones de baja volatilidad
El efecto de la volatilidad en los rendimientos finales explica, junto con algunos aspectos de la naturaleza del comportamiento, la anomalía aparente por la cual las acciones con menor volatilidad tienden en el tiempo a superar a las que tienen una alta volatilidad, lo que contradice una de las premisas fundamentales de la teoría de la inversión en relación a que a mayor riesgo: mayor rendimiento esperado.
Este fenómeno, también llamado anomalía de la baja volatilidad, se debe al hecho de que las acciones de baja volatilidad, cuyos precios no tienden a sufrir fuertes caídas en el tiempo, no descuentan el efecto negativo de la capitalización, como sí les ocurre a las acciones de alta volatilidad. Esto tiene efectos positivos sobre el rendimiento a largo plazo.
En los últimos 15 años en Estados Unidos el índice de las acciones de baja volatilidad tuvo un rendimiento anual del 9,2%, frente al 6,60% del S&P 500.
Falkenstein nos hace ver que, incluso si la media aritmética de los rendimientos de bonos con una alta beta es superior que la del S&P, debido a que la volatilidad erosiona la inversión, el rendimiento es inferior cuando se considera el rendimiento geométrico.
Los ETF apalancados como amplificadores de volatilidad
La volatility drag adquiere una importancia central en el análisis de los instrumentos financieros que amplifican la volatilidad de los rendimientos como son los ETFs apalancados. Estos ETFs tienen como objetivo multiplicar la amplitud de los movimientos diarios del índice subyacente. Por ejemplo, los ETFs apalancados 3x intentan devolvernos sobre una base diaria, el rendimiento del subyacente multiplicado por 3.
Para este tipo de ETF una variación diaria positiva y negativa de la misma cantidad (x) del índice subyacente, daría lugar a una variación del ETF igual a:
(1 – 3x) * (1 + 3x) = 1 – 9x2
Suponiendo x = 20%, + 20% y - 20% consecutivo daría lugar a una un volatility drag del 36%. El ETF, a partir de un precio inicial hipotético de 100, se reduciría a 64! Esto, frente a un rendimiento promedio aritmético, en los dos días igual a cero.




