Con los ratios anteriores podemos evaluar la bondad de un sistema de trading. Lo siguiente es lo que yo considero que son las características de un sistema que merece la pena ser operado con dinero real:
- Tiene menos de 4 o 5 parámetros (es sencillo)
- Está evaluado en suficientes datos. Al menos 2 años si es intradiario y al menos 10 años si es diario. Como mínimo buscaremos unas 200 operaciones.
- Genera ganancias año tras año, aunque sean limitadas o Es robusto; variando ligeramente sus parámetros sus resultados varían ligeramente; es decir, no está construido sobre un pico de ganancia.
- Funciona en la mayoría de instrumentos con características similares (otra forma de robustez).
- Ratio de Sharpe >= 1 (menor no implica que sea un mal sistema sino que habrá que seguir investigando)
- Recovery Factor >= 6
- MSD < 30%
- Profit Factor >= 2
En cuanto al porcentaje de aciertos y payoff ratio es una cuestión de preferencias, siempre y cuando entre los dos se consiga una combinación que genere resultados positivos. Más adelante veremos la expectativa y cómo combinar adecuadamente estos datos.
A la hora de diseñar un sistema no es necesario conseguir una rentabilidad anual demasiado elevada sino que se mantenga en el tiempo. Suponga que su sistema genera una rentabilidad del 25% anual. Si consigue mantenerlo así solamente 3 años duplicará su capital, y si opera durante 21 años un sistema así, partiendo de 10.000 euros, al final conseguirá 1 millón de euros. No busque un sistema que le genere un 500% el año próximo, busque uno estable y sencillo, que pueda funcionar en varios mercados diferentes porque si es así probablemente siga funcionando dentro de unos años.
Robustez
Antes de explicar el método científico conviene hablar de la robustez de un sistema. Vamos a definir la robustez como la capacidad de un sistema para funcionar en otros mercados diferentes del que fue diseñado. Cuantos más mercados terminen en ganancias en nuestro sistema, más robusto será éste. En Kaufman “New trading systems and methods” el autor utiliza esta definición de robustez y explica que si un sistema diseñado para el SP500 da pérdidas en el Nasdaq entonces es que no es robusto y por tanto no es fiable. Puede estar sobreoptimizado y adaptado a los datos históricos y por tanto no tendrá poder predictivo. Un buen sistema debe ser robusto y funcionar en mercados equivalentes. Así, un sistema para Forex (divisas) no tiene porqué funcionar bien con acciones o con índices. Pero un buen sistema aplicado sobre 20 materias primas debería dar ganancias en el mayor número posible de ellas, ya que son instrumentos equivalentes. Si genera beneficios en 17 tendría entonces una robustez del 17/20=85%. Los sistemas clásicos y los mejores sistemas suelen tener una robustez entre el 70 y el 100%. En el siguiente documento se explican las pruebas de robustez que se hicieron para diseñar un sistema sobre materias primas: El sistema XINV para materias primas
El hecho de que un sistema funcione en varios mercados nos ayuda adicionalmente a evitar el error de extraer demasiadas conclusiones de una muestra muy pequeña de datos por probar un sistema solamente en un mercado. Incluso si podemos probar estadísticamente que un sistema es fiable, si no es robusto no lo querremos operar porque podríamos estar ante una sobreoptimización o ante un error de diseño.
La prueba estadística de un sistema
Como se ha explicado ya, todo consiste en ser capaces de poder demostrar al menos al 95% de confianza que no es cierto que nuestro sistema tenga una ganancia promedio de cero euros.
Para comparar la media de nuestro sistema con cero utilizamos el estadístico t de student, que se aplica cuando la población estudiada sigue una distribución normal pero el tamaño de la muestra es pequeño. Esta es la misma prueba que utilizan los laboratorios farmacéuticos para comprobar la efectividad de un medicamento de forma científica.
Desde un punto de vista práctico no hace falta saber toda la teoría detrás de la prueba de student. Todo se reduce a calcular el estadístico t que arroja la ganancia de nuestro sistema y si es mayor que un valor de referencia entonces nuestro sistema será fiable estadísticamente.
El estadístico t se calcula a partir de la media y desviación de las ganancias individuales. Conviene dividir entre el riesgo de cada operación individual para que el resultado sea independiente del tamaño de la posición. Así, si tenemos las siguientes operaciones.
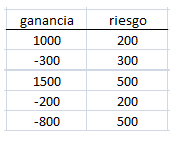
Dividimos cada una entre el riesgo que se asumió al abrirla y el resultado será una hilera de ganancias y pérdidas ecualizadas en términos de riesgo. Así en este caso tendríamos.
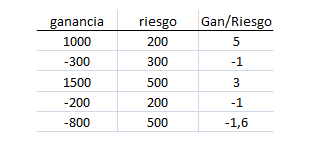

Aquí la ganancia media es de 0.88R (R significa múltiplos del riesgo) y la desviación es de 2.945R. El cociente entre estos dos valores será muy importante ya que nos dirá lo que gana un sistema con respecto al riesgo de operarlo. Este cociente forma parte del estadístico t, de forma que el estadístico t se define así:
t = (Media/Desv)*raíz(Num operaciones)
en este caso sería: 0.88/2.945*raíz(5)=0.668
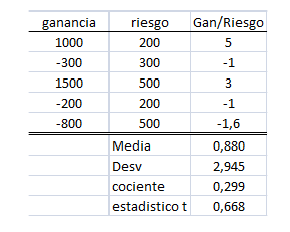
Este valor, t=0.668 debe compararse con una tabla de valores significativos de t al grado de confianza que queramos confirmar (normalmente el 95%). Si buscamos el valor de t para 5 datos y 95% de confianza encontramos t=2.015. Por consiguiente este sistema no sería estadísticamente fiable al 95% de confianza. Su estadístico t es menor que el t(5,95%).
En esta prueba con solo 5 operaciones es bastante lógico haber encontrado que el sistema no es diferente de cero o que no es rentable, o mejor dicho, que no podemos negar que su ganancia media sea nula. En general se pide que cualquier muestra de datos contenga al menos 30. Esto es debido a que el error de muestreo es proporcional a 1/raíz(N), siendo N el número de operaciones, y por eso a partir de 30 este error empieza a ser aceptable (con 30 es del 18%). Por otra parte, cuando estimamos la desviación de la población a partir de la desviación de la muestra tenemos un error que es raíz(N/(N-1)) y que es más pequeño cuantas más muestras tengamos.


Afortunadamente hay paquetes de software que lo calculan todo automáticamente y nos dicen si se superan los test estadísticos. Uno de ellos es MSA o Market System Analyser, que es un software muy bueno para evaluar sistemas. Más adelante veremos todo esto sobre un sistema real.
¿Un sistema o un conjunto de sistemas?
Una vez se ha diseñado un sistema de trading rentable se tienen las bases para una operativa regular que genere beneficios. Sin embargo no es tan sencillo ya que todos los sistemas pasan por periodos de drawdown que en algunos casos pueden durar incluso años. Diversificar por mercados no es la solución ya que el mismo sistema dará las señales de forma simultánea en los instrumentos a operar, con lo cual la correlación entre elementos será tan alta que dará lo mismo tener mucho riesgo en una posición que poco en muchas posiciones. El drawdown será el mismo. Para evitar esto lo mejor es combinar sistemas de forma que cuando unos vayan mal otros vayan bien y la curva de capital resultante nos evite pasar mucho tiempo en pérdidas.
Lo bueno de combinar sistemas es que si tienen una lógica diferente (si no fuera el caso no hablaríamos de sistemas diferentes) entonces sus señales de entrada y salida vendrán en momentos diferentes de forma que la ganancia total al final será una suma algebraica de beneficios pero el drawdown no será una suma de drawdowns individuales porque cuando un sistema puede estar en drawdown el otro puede estar en ganancias, produciendo un drawdown conjunto pequeño o nulo. Se entiende mejor si imaginamos dos curvas de capital diferentes y las sumamos. La ganancia total al final de la curva será la suma, pero por el camino ambas curvas se combinan y normalmente generan menos drawdown que de forma individual. En el peor de los casos los drawdown vendrían a la vez, pero esto es poco frecuente. De forma práctica podemos decir que cuando se combinan sistemas la ganancia es la suma y el drawdown es un valor intermedio entre los sistemas.
Para demostrar todas estas afirmaciones veamos un ejemplo. A continuación tenemos las estadísticas del sistema para el Nasdaq100 que está funcionando en el servicio de recomendaciones onda4.com para dar señales de entrada y salida. Esta simulación se hace en el periodo 2002- 2012 con un futuro grande (100 dólares por punto). Las estadísticas de estos 10 años son:
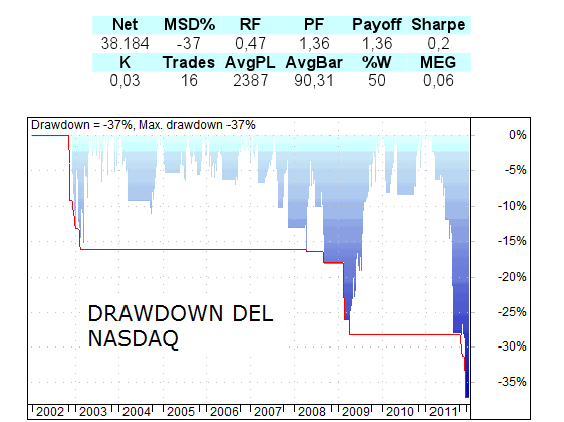
Figura 3. Drawdown individual del sistema sobre el Nasdaq100.
El mayor valor ocurre al final del periodo de simulación y es de un 37%.
Este sistema opera solo en el lado largo, aprovechando el sesgo alcista del mercado a largo plazo. Vamos a ver qué pasaría si lo combinamos con el sistema del DAX, un sistema que opera tanto el lado largo como el lado corto del mercado.


Combinando sistemas
Pues bien, ha llegado el momento de combinar los dos sistemas en uno solo. Esto se puede hacer fácilmente en Amibroker con un poco de código. Este software es extremadamente potente y nos permitirá hacer todo tipo de pruebas que se nos ocurran.

Como vemos la ganancia es la suma algebraica de las ganancias individuales de los dos sistemas. Y el drawdown es un valor intermedio. Mejor que el del Nasdaq solo y peor que el del DAX solo. Es un 28% que entra dentro de lo aceptable. Es decir, al combinar los dos sistemas ahora tenemos un sistema que gana lo mismo que los dos juntos pero con un drawdown intermedio. ¡Es una combinación beneficiosa!

Fíjese que el resto de métricas también toma un valor intermedio, como sería el caso del Recovery Factor, Profit Factor, y por supuesto el porcentaje de aciertos, que al combinarse nos da un valor medio del 40%, siendo el del Nasdaq del 50 y el del DAX del 37%.
Algo muy interesante es lo que sucede con el ratio K. El ratio nos dice lo buena que es la curva de capital. Lo suave que es. Se calcula dividiendo la pendiente de subida de la curva entre su desviación estadística. Es un ratio aceptado en la industria del trading como buen indicador de la “operabilidad” de un sistema.



